Adik-adik berikut ringkasan materi Matematika (Bilangan Bulat) yang bisa kalian pelajari... semoga materi ini bermanfaat...
1. Pengertian Bilangan Bulat
Bilangan bulat terdiri dari
- bilangan asli : 1, 2, 3, ...
- bilangan nol : 0
- bilangan negatif : ..., -3, -2, -1
Bilangan Bulat dinotasikan dengan : B = {..., -3, -2, -1, 0, 1, 2, 3, ...}
Bilangan lain yang berada dalam bilangan bulat, di antaranya adalah bilangan:
a. Cacah : C = {0, 1, 2, 3, 4, ...}
b. Ganjil : J = {1, 3, 5, 7, ...}
c. Genap : G = {2, 4, 6, 8, ...}
d. Cacah Kuadrat : K = {0, 1, 4, 9, ...}
e. Prima : {2, 3, 5, 7, 11, ...}
2. Membandingkan Bilangan Bulat
Dengan memperhatikan tempat pada garis bilangan, dapat kita nyatakan (dalam contoh) bahwa :
a. 7 > 4, karena 7 terletak di sebelah kanan 4,
b. (-5) < 2, karena (-5) terletak di sebelah kiri 2, dan lain sebagainya.
3. Penjumlahan dan Sifatnya
Salah satu Rumus penting :
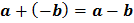
Contoh : 7 + (-10) = 7 - 10 = -3
Sifat-sifatnya :
a. Komutatif :
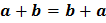
b. Asosiatif :
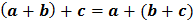
c. Tertutup :
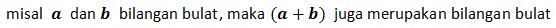
d. Memiliki identitas :

e. Invers penjumlahan :
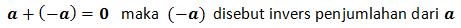
4. Pengurangan
Pengurangan merupakan lawan (invers) dari penjumlahan.
Rumus :
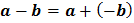
Contoh : 8 - (-2) = 8 + 2 = 10
5. Perkalian dan Sifatnya
contoh :
3 x (-2) = (-2) + (-2) + (-2)

Sifat-sifat :

6. Pembagian
Pembagian adalah kebalikan (invers) dari perkalian.
Rumus :
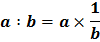
7. Perpangkatan dan Sifat

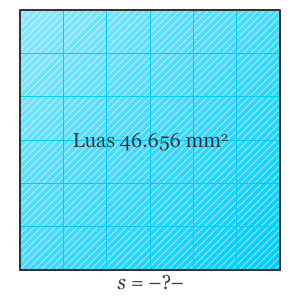
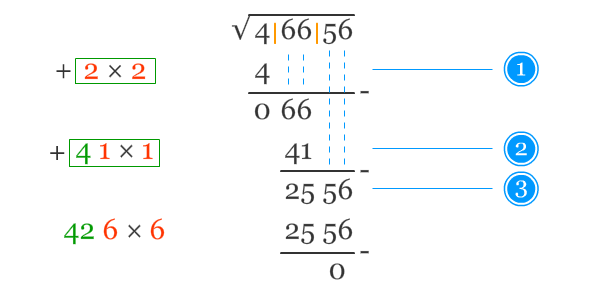
8. Akar Pangkat Dua dan Akar Pangkat Tiga

1. Pengertian Bilangan Bulat
Bilangan bulat terdiri dari
- bilangan asli : 1, 2, 3, ...
- bilangan nol : 0
- bilangan negatif : ..., -3, -2, -1
Bilangan Bulat dinotasikan dengan : B = {..., -3, -2, -1, 0, 1, 2, 3, ...}
Bilangan lain yang berada dalam bilangan bulat, di antaranya adalah bilangan:
a. Cacah : C = {0, 1, 2, 3, 4, ...}
b. Ganjil : J = {1, 3, 5, 7, ...}
c. Genap : G = {2, 4, 6, 8, ...}
d. Cacah Kuadrat : K = {0, 1, 4, 9, ...}
e. Prima : {2, 3, 5, 7, 11, ...}
2. Membandingkan Bilangan Bulat
Dengan memperhatikan tempat pada garis bilangan, dapat kita nyatakan (dalam contoh) bahwa :
a. 7 > 4, karena 7 terletak di sebelah kanan 4,
b. (-5) < 2, karena (-5) terletak di sebelah kiri 2, dan lain sebagainya.
3. Penjumlahan dan Sifatnya
Salah satu Rumus penting :
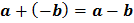
Contoh : 7 + (-10) = 7 - 10 = -3
Sifat-sifatnya :
a. Komutatif :
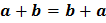
b. Asosiatif :
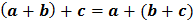
c. Tertutup :
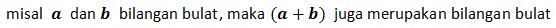
d. Memiliki identitas :

e. Invers penjumlahan :
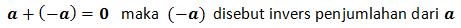
4. Pengurangan
Pengurangan merupakan lawan (invers) dari penjumlahan.
Rumus :
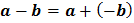
Contoh : 8 - (-2) = 8 + 2 = 10
5. Perkalian dan Sifatnya
contoh :
3 x (-2) = (-2) + (-2) + (-2)

Sifat-sifat :

6. Pembagian
Pembagian adalah kebalikan (invers) dari perkalian.
Rumus :
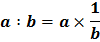
7. Perpangkatan dan Sifat

8. Akar Pangkat Dua dan Akar Pangkat Tiga